题解 APA 算法编程协会内部第三次月赛 —— “类天梯模拟赛” | 我有昕想法

本篇题解所使用的语言是C++，部分其他语言的选手可能需要理解做法后自行编写对应语言的代码。

L1-1 等号警长的求助

题目背景

你是数字之城最著名的侦探——派大饼。一天，等号警长向你发来求救短信，你需要立即回他消息。

题目描述

What on earth is going on??!

请你输出这句话帮他回复短信。

输入格式

无

输出格式

一行字符串。

输入样例

无

输出样例

1	What on earth is going on??!

题解

输出时注意避免三字符组转义即可。

代码

#include<bits/stdc++.h>
using namespace std;
int main()
{
    cout<<"What on earth is going on\?\?!";
    return 0;
}

L1-2 数字之城的谜团

题目背景

质数：只能被1和自己整除的数。
合数：除了能被1和它本身整除，还能被其他的正整数整除。

你是数字之城最著名的侦探——派大饼。通过新闻得知，城内出现了许多数字干尸，遍布城市各个区域，这些受害者都是大于0的整数。很明显，数字之城出现了吸血鬼。案件十分棘手，你的好朋友等号警长找到了你，希望你能帮他的忙。你们统计了所有干尸，发现存在几名失踪人员。虽然你最近一直在调查这些失踪人员，但还是把警长发给你的线索看了一下，你得出了一个结论，所有失踪人员都是绝对质数。

题目描述

所谓绝对质数，是指一个本身是质数且通过拆分无法将其拆成不是质数的数。

以下是一些例子：

2是绝对质数，因为它是质数且无法被拆分；
4不是绝对质数，因为它不是质数；
13不是绝对质数，虽然它是质数，但是可以拆分为1和3，其中1不是质数；
23是绝对质数，因为它是质数，且拆分为2和3后得到的也是质数；
137不是绝对质数，虽然它是质数，但可以拆分为1和37，其中1不是质数。（注意，虽然拆分为13和7满足划分完是质数，但是要所有拆分都无法拆出不是质数的数；此外，1、3、7的拆分方式也能说明他不是绝对质数）

现在，等号警长希望给你个名单，你需要快速告诉等号警长名单上的人员会是干尸还是失踪人员，以方便警长救援。

输入格式

第一行一个数字 $ T $ ，表示名单上人员的数量。

第二行到第 $ T+1 $ 行，每行一个数字，表示名单上的数字 $n_i$ 。

输出格式

共 $ T $ 行，每行一个字符串，如果 $n_i$ 是干尸，则输出 ganshi ，否则输出 shizong 。

输入样例

输出样例 1

shizong
ganshi
ganshi
shizong
ganshi

数据范围

$ 1 \leq T \leq 10^6 $
$ 1 \leq n_i \leq 10^9 $

题解

可以手动模拟一下，很容易发现一位的绝对质数是：2、3、5、7。

对于两位的绝对质数，只能由上面四个数组合得到，也就是从22、23、25、27、32、33、35、37、52、53、55、57、72、73、75、77这16个数中得到。
其中22、32、52、72可以被2整除不是质数；25、35、55、75可以被5整除不是质数；33和77可以被11整除不是质数；27和57可以被3整除不是质数。即两位的绝对质数只有23、37、53、73。

三位的绝对质数要满足前两个数是两位的绝对质数且后两个数是两位的绝对质数，所以只能第二位和第三位只能是3和7。
通过符合上述条件的组合，能够得到的数只有237、373、537、737这四个数。
其中237和537可以被3整除不是质数，737可以被11整除不是质数。即三位的绝对质数只有373。

由于四位的绝对质数要满足前三个数是三位的绝对质数且后两个数是两位的绝对质数，所以不能存在四位的绝对质数。同时，也就不存在更多位数的绝对质数。

因此，打表判断即可通过。

代码

#include<bits/stdc++.h>
using namespace std;
int T;
int n;
bool pd[1000];
void init()
{
    memset(pd,0,sizeof(pd));
    pd[2]=true;
    pd[3]=true;
    pd[5]=true;
    pd[7]=true;
    pd[23]=true;
    pd[37]=true;
    pd[53]=true;
    pd[73]=true;
    pd[373]=true;
}
bool panduan(int n)
{
    if(n>=1000)return false;
    return pd[n];
}
int main()
{
    init();
    scanf("%d",&T);
    while(T-->0)
    {
        scanf("%d",&n);
        printf("%s\n",panduan(n)?"shizong":"ganshi");
    }

    return 0;
}

L1-3 奇怪的两个骰子

题目背景

你和等号警长找到了失踪人员关押的地方，但是门口有一个智能锁，锁上有两个奇怪的骰子。智能锁提示，只有通过多次投掷，将投掷的和正确扔到指定的数字，才能开锁。等号警长希望知道他一次就打开门锁的概率。

题目描述

换句话来说，现在有两个奇怪的骰子，你需要投掷它们 $n$ 次，求所有投掷结果加和等于指定的数字 $m$ 的概率。

这两个骰子的点数分别是：

骰子1：1,2,2,3,3,4
骰子2：1,3,4,5,6,8

由于概率可能为小数，但是等号警长想看到确切的值，因此请将小数转为最简分数的形式输出。

输入格式

共一行，两个数字 $n$ 和 $m$ ，为投掷次数和指定的数字。

输出格式

共一行，为可能的概率。

输入样例

2 4

输出样例

1/1296

数据范围

$ 1 \leq n \leq 10 $

题解

这两个骰子也叫西克曼骰子，点数分别是1,2,2,3,3,4和1,3,4,5,6,8，概率和抛出两个正常骰子是一样的。因此直接dp就行。

本来计划在这里搞一个乘法逆元，但是考虑天梯几乎没有考过乘法逆元，因此没有这么出，但是我还是给出乘法逆元版本的结果。

本题代码

#include<bits/stdc++.h>
using namespace std;
const int p[13]={0,0,1,2,3,4,5,6,5,4,3,2,1};
long long gcd(long long a,long long b)
{
    return b==0?a:gcd(b,a%b);
}

long long f[15][125];
int n,m; 
int main()
{
    cin>>n>>m;
    if(m<2*n||m>12*n)
    {
        cout<<0<<endl;
        return 0;
    }
    f[0][0]= 1;
    for(int i=1;i<=n;i++)
    {
        for(int j=2*i;j<=12*i;j++)
        {
            f[i][j]=0;
            for(int k=2;k<=12;k++)
            {
                if(j-k>=2*(i-1)&&j-k<=12*(i-1))
                {
                    f[i][j]+=f[i-1][j-k]*p[k];
                }
            }
        }
    }

    long long ans = f[n][m];
    long long sum = 1;
    for(int i=0;i<n;i++)
    {
        sum*=36;
    }

    long long g=gcd(ans,sum);
    ans/=g;
    sum/=g;
    cout<<ans<<"/"<<sum<<endl;
    return 0;
}

模意义下的代码

#include<bits/stdc++.h>
using namespace std;
const long long mod=998244353;
const int p[13]={0,0,1,2,3,4,5,6,5,4,3,2,1};
long long qpow(long long a,long long b)
{
    long long res=1;
    while(b)
    {
        if(b&1)res=res*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return res;
}
long long f[1005][12005];
int n,m; 
int main()
{
    cin>>n>>m;
    if(m<2*n||m>12*n)
    {
        cout<<0<<endl;
        return 0;
    }
    f[0][0]= 1;
    for(int i=1;i<=n;i++)
    {
        for(int j=2*i;j<=12*i;j++)
        {
            f[i][j]=0;
            for(int k=2;k<=12;k++)
            {
                if(j-k>=2*(i-1)&&j-k<=12*(i-1))
                {
                    f[i][j]=(f[i][j]+f[i-1][j-k]*p[k])%mod;
                }
            }
        }
    }

    long long ans = f[n][m];
    long long sum = 1;
    for(int i=0;i<n;i++)
    {
        sum=sum*36%mod;
    }

    long long inv=qpow(sum,mod-2);
    long long res=ans*inv%mod;
    cout<<res<<endl;
    return 0;
}

L1-4 逃脱的最佳位置

题目背景

你和等号警长打开了门锁看到了失踪的人员，然而，邪恶的反派居然在房间中设置了反物质炸弹！你意识到你们无法抵抗这强大的力量——聚变和湮灭的混沌，所以必须要躲过反物质炸弹！

题目描述

反派在这里设置的反物质炸弹是一个精心设计过的超大粒子圆环，物质粒子和反物质粒子的数量相等。随着你们打开房间，物质粒子开始与反物质粒子进行合并。如果物质粒子顺时针方向上的下一个是反物质粒子，那么二者才能合并，然后“砰”的一声湮灭合并路径上的生物并且消失。剩下的粒子会收缩成小一点儿的圆环然后不断重复这个过程直到结束。

你需要找到一个合适的位置，来保证你们不会被湮灭。

具体来说，你将拿到一行字符串表示顺时针顺序下的粒子圆环，因为有 $n$ 个粒子，所以有 $n$ 个站位。

例如粒子圆环 -++- ，一共四个粒子所以有四个位置，分别为站第一个粒子上一个空（称为位置0）、第一个粒子下一个空（称为位置1）、第二个粒子下一个空（称为位置2）和第三个粒子下一个空（称为位置3）。（第四个粒子下一个空和第一个粒子上一个空是一样的。）

即 0-1+2+3- 这样，一共四个位置可选。

对这个粒子圆环，第三个粒子与第四个粒子合并，湮灭了位置3上的人；第二个粒子和第一个粒子合并，湮灭了位置2和位置0上的人。因此只有位置1可选。

输入格式

第一行一个数字 $n$ 表示粒子数量。

第二行为 $n$ 个字符，表示粒子，物质粒子为 + ，反物质粒子为 - 。

输出格式

共一行一个数字，为最佳的位置。

输入样例 1

1
2

4
-++-

输出样例 1

输入样例 2

1 2	10 ++-++----+

输出样例 2

数据范围

对于40%的数据， $n \leq 50$ ；
对于70%的数据， $n \leq 10^3$ ；
对于100%的数据， $ 2 \leq n \leq 10^6 $ 。
数据保证合法，站位存在且唯一。

样例解释

对于样例1，湮灭过程如下：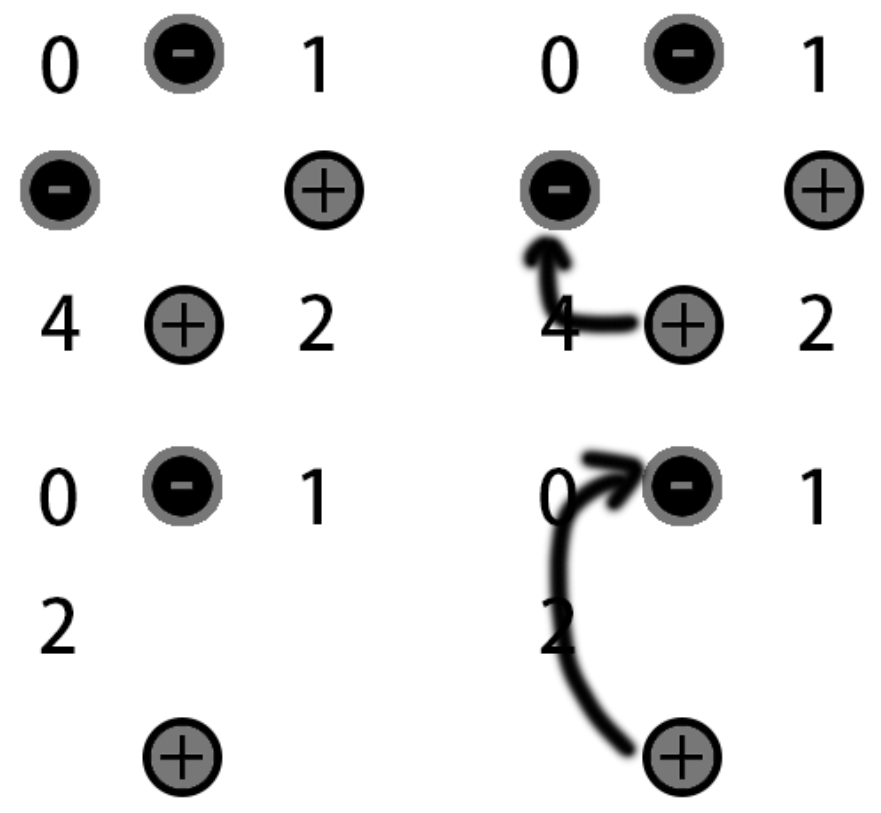
样例1

对于样例2，湮灭过程如下：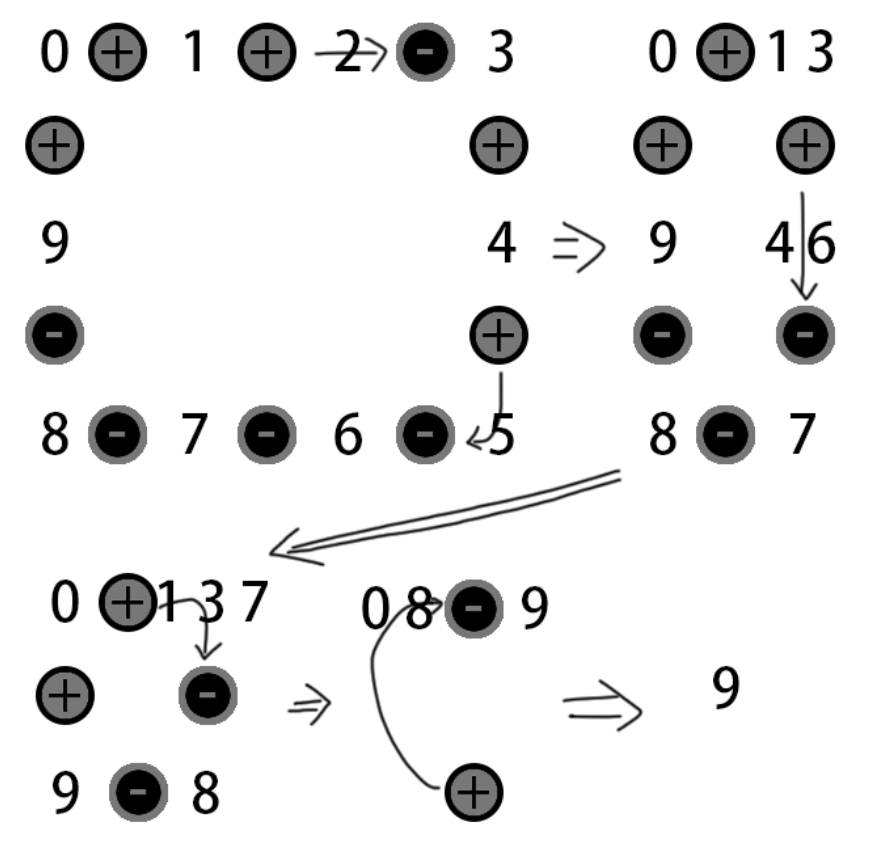
样例2

题解

我们把能够合并到两个粒子放在同一层里，把被包含在其他粒子之间的粒子放在更高的一层里，对于两个样例，空隙的层数如下：

 1|      3
  |     + -
 0|0   2
  | - +
-1|  1

 3|          5
  |         + -
 2|    2   4   6
  |   + - +     -
 1|  1   3       7
  | +             -
 0|0               8
  |                 - +
-1|                  9

显然，山峰会直接合并，山谷处最安全，所以直接转换为层数加减指令寻找最低点即可。

代码

#include<bits/stdc++.h>
using namespace std;
string s;
int n;
int mins=0,mini=0,mint=1;
int nows=0;
int main()
{
    cin>>n;
    cin>>s;
    for(int i=0;i<n;i++)
    {
        if(s[i]=='+')
        {
            nows++;
        }
        if(s[i]=='-')
        {
            nows--;
            if(nows<mins)
            {
                mins=nows;
                mini=i+1;
                mint=1;
            }
            else if(nows==mins)
            {
                mint++;
            }
        }
    }
    cout<<mini<<endl;
    return 0;
}